How To Find Margin Of Error Without Sample Size

When yous demand to notice a statistical sample mean (or boilerplate), you besides need to written report a margin of error, or MOE, for the sample mean. You can too calculate the margin of mistake of a sample proportion, which is the amount of "successes" in a sample compared to the whole. The general formula for the margin of error for the sample mean (bold a certain condition is met — run into below) is

is the population standard difference, n is the sample size, and z* is the appropriate z*-value for your desired level of confidence (which you tin detect in the post-obit table).

z*-Values for Selected (Percent) Conviction Levels
Percentage Confidence	z*-Value
fourscore	1.28
90	1.645
95	ane.96
98	2.33
99	ii.58

Notation that these values are taken from the standard normal (Z-) distribution. The area between each z* value and the negative of that z* value is the confidence percentage (approximately). For instance, the area between z*=1.28 and z=-one.28 is approximately 0.80. This chart can be expanded to other conviction percentages besides. The nautical chart shows only the confidence percentages most usually used.

Here are the steps for calculating the margin of error for a sample mean:

1. Find the population standard divergence and the sample size, due north.

   The population standard deviation, σ, will exist given in the problem.

2. Divide the population standard deviation by the square root of the sample size.

   

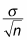
   gives y'all the standard error.

3. Multiply by the appropriate z*-value (refer to the to a higher place table).

   For instance, the z*-value is i.96 if yous want to be virtually 95% confident.

The condition you need to meet to use a z*-value in the margin of fault formula for a sample mean is either: ane) The original population has a normal distribution to start with, or 2) The sample size is large enough then the normal distribution can be used (that is, the Central Limit Theorem applies).

In general, the sample size, n, should be above most 30 in order for the Central Limit Theorem to be applicable. Now, if it'due south 29, don't panic — 30 is not a magic number, it's simply a full general dominion of thumb. (The population standard deviation must be known either way.)

Hither's an case: Suppose you lot're the manager of an ice cream shop, and you're training new employees to be able to fill the big-size cones with the proper amount of ice cream (10 ounces each). Y'all want to approximate the average weight of the cones they make over a one-day period, including a margin of error. Instead of weighing every single cone made, you lot enquire each of your new employees to randomly spot check the weights of a random sample of the large cones they brand and record those weights on a notepad. For n = 50 cones sampled, the sample mean was constitute to be 10.3 ounces. Suppose the population standard departure is 0.6 ounces.

What's the margin of error? (Assume yous desire a 95 percent level of conviction.) It's calculated this manner:

So to written report these results, y'all say that based on the sample of l cones, you gauge that the average weight of all big cones made past the new employees over a one-24-hour interval catamenia is 10.3 ounces, with a margin of error of plus or minus 0.17 ounces. In other words, the range of probable values for the average weight of all large cones made for the 24-hour interval is estimated (with 95 percent confidence) to be betwixt x.30 – 0.17 = 10.13 ounces and 10.thirty + 0.17 = 10.47 ounces. The new employees appear to be giving out too much water ice cream (although you're probably getting groovy reviews from your customers!).

Notice in this instance, the units are ounces, non percentages. When working with and reporting results nigh data, e'er think what the units are. Also, be sure that statistics are reported with their right units of measure, and if they're not, ask what the units are.

In cases where n is as well modest (in general, less than 30) for the Central Limit Theorem to be used, but you still think the data came from a normal distribution, y'all can use a t*-value instead of a z*-value in your formulas. A t*-value is ane that comes from a t-distribution with north – 1 degrees of freedom. In fact, many statisticians become ahead and use t*-values instead of z*-values consistently, because if the sample size is large, t*-values and z*-values are approximately equal anyway.

In addition, for cases where you lot don't know the population standard difference, σ, you can substitute information technology with s, the sample standard deviation; from there you use a t*-value instead of a z*-value in your formulas as well.

Nigh This Article

Nigh the volume author:

Deborah Rumsey, PhD, is an auxiliary kinesthesia fellow member and program specialist in department of statistics at The Ohio Country Academy. An writer of several Dummies books, she is a fellow of the American Statistical Clan.

This article tin be institute in the category:

• Statistics ,

How To Find Margin Of Error Without Sample Size,

Source: https://www.dummies.com/article/academics-the-arts/math/statistics/how-to-calculate-the-margin-of-error-for-a-sample-mean-169842

Posted by: buserhision.blogspot.com

Share this post